= 접근 방법 =
NxN 배열 A
A[i][j] = i * j
이 수를 일차원 배열 B에 넣으면 B의 크기는 NxN이 된다.
B[k]를 구해보자
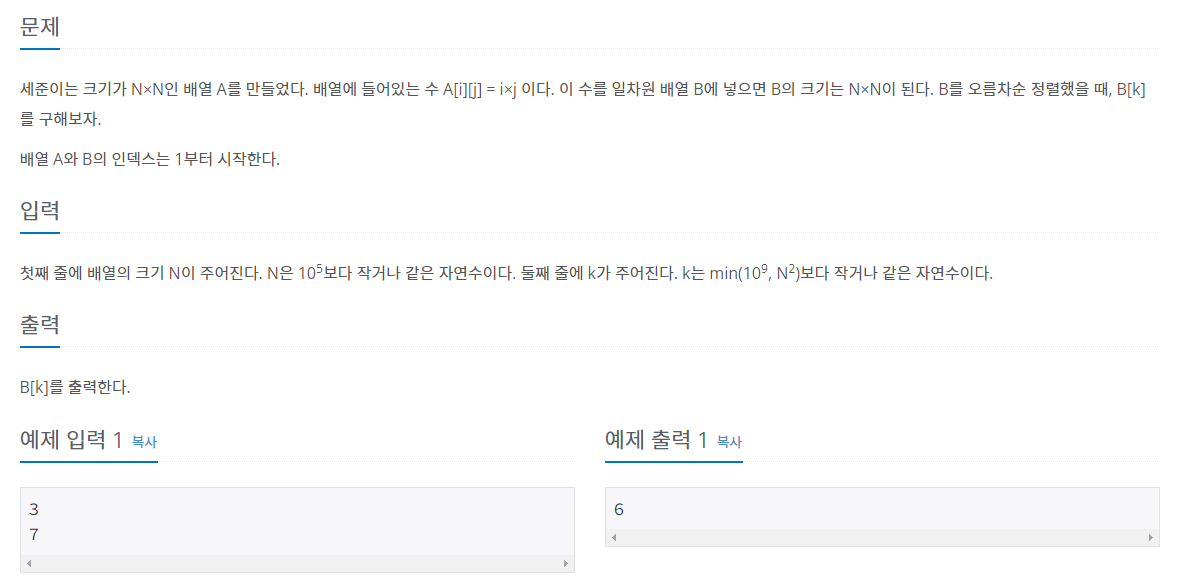
N = 3, B = 7일 때 b[7] = 6이 문제에서 주어졌다.
문제를 그래도 만들어보자,
int[][] A = new int[3][3]

그동안 우리가 해왔던 이분 탐색 문제들은 단순하게 주어진 값을 이용해서
반으로 나누는 식으로 어떻게든 2중 for문 시간 복잡도 O(N^2)이 아닌, O(logN)형식으로 만들면 되는 거였다.
이 문제가 어려운 이유는?
=> 지금까지 풀어왔던 틀에서 완전히 벗어나 새로운 규칙을 발견하고 응용해야 된다.
입력) 배열의 크기 N이 주어진다. N은 105보다 작거나 같은 자연수
이 문장을 봤을 때, 순수하게 배열을 그대로 만든다면 시간이 엄청 오래 걸릴 것이다.
결국 이 배열을 만드는 것도 2중 for문을 이용해서 만들어야 하기 때문이다.
따라서 배열을 직접 생성해서 해결하는 문제가 아니라, 이 배열의 규칙을 찾고 효율적으로 내가 원하는 값을 뽑아내야 한다.

N = 3일 때, 배열을 만들어보고 일차원 배열 B를 생성해서 오름차순으로 해보자

B[7] = 6이라는 값을 얻어낼 때, 어떻게 6을 그대로 뽑아낼 수 있을까?
x = 6이라고 가정할 때, x보다 작은 숫자가 최소 7개 존재한다 라는 식을 만들 수 있다.
x = 4 => x보다 작거나 같은 숫자는 6개
이런식으로 식을 뽑아내야 이 문제를 해결할 수 있다.
그럼 x의 범위는 어떻게 될까?
1 <= x <= K라는 범위까지 만들어낼 수 있음!
이 식을 이용해서 해결하자
여기서 LowerBound, UpperBound 둘 중 하나를 선택해야 되는데 LowerBound를 이용해서 해결해야 된다.
그 이유는 최솟값을 구해야 되기 때문이다.
x = 6일 때, k = 7 or k = 8을 만족하기 때문에, 중복값 중 가장 작은 값을 선택하려면 LowerBound 방식을 이용해야 한다.
근데 배열을 안 만들고 어떻게 B의 값을 구할 수가 있을까?
A배열을 만들었을 때 규칙을 보면 구구단이 보인다. 이 방식을 이용해서 해결하자.
ex) 1 ~ 9단까지 구구단에서 8이하의 수를 찾으려면 어떻게 해야 될까?
8 / 1 => 8개
8 / 2 => 4개
8 / 3 => 2개
8 / 4 => 2개
8 / 5 => 1개
8 / 6 => 1개
8 / 7 => 1개
8 / 8 => 1개
8 / 9 => 0개
이런식으로 찾을 수 있다.
그럼 우리 문제에 적용을 해보자
B[7] = 6이다.
6보다 작은 수의 개수를 찾아야 된다.
N = 3이기 때문에 3단이라고 가정하고
6 / 1 => 6
6 / 2 => 3
6 / 3 => 2
이렇게 하면 안 된다 왜냐하면 우리는 1x1, 1x2, 1x3 N까지의 범위를 생각해야 되기 때문이다.
6 / 1 => min(6, N)
6 / 2 => min(3, N)
6 / 3 => min(2, N)을 이용하자.
1 ~ K가 주어졌고, 이 두 수로 중간값을 만들어 K를 만족하는 중간값을 찾으면 된다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; public class ReMain2 { public static void main(String[] args) throws IOException { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); int n = Integer.parseInt(br.readLine()); int k = Integer.parseInt(br.readLine()); long start = 1; long end = k; while (start < end) { long count = 0; long mid = (start + end) / 2; for (int i = 1; i <= n; i++) { count += Math.min(mid / i, n); } if (count > k) { end = mid; } else if (count == k) { end = mid; } else if (count < k) { start = mid + 1; } } System.out.println(start); } } | cs |
'백준 오답노트 > 이분 탐색' 카테고리의 다른 글
| 백준 - 이분 탐색 2110번 공유기 설치 / 풀이, 오답 (0) | 2023.01.17 |
|---|---|
| 백준 - 이분 탐색 2805번 나무 자르기 / 풀이, 오답 (0) | 2023.01.09 |
| 백준 - 이분 탐색 1654번 랜선 자르기 / 풀이,오답 (0) | 2023.01.09 |
| 백준 - 이분 탐색 10816 숫자 카드2 문제 / 복습 (0) | 2023.01.05 |
