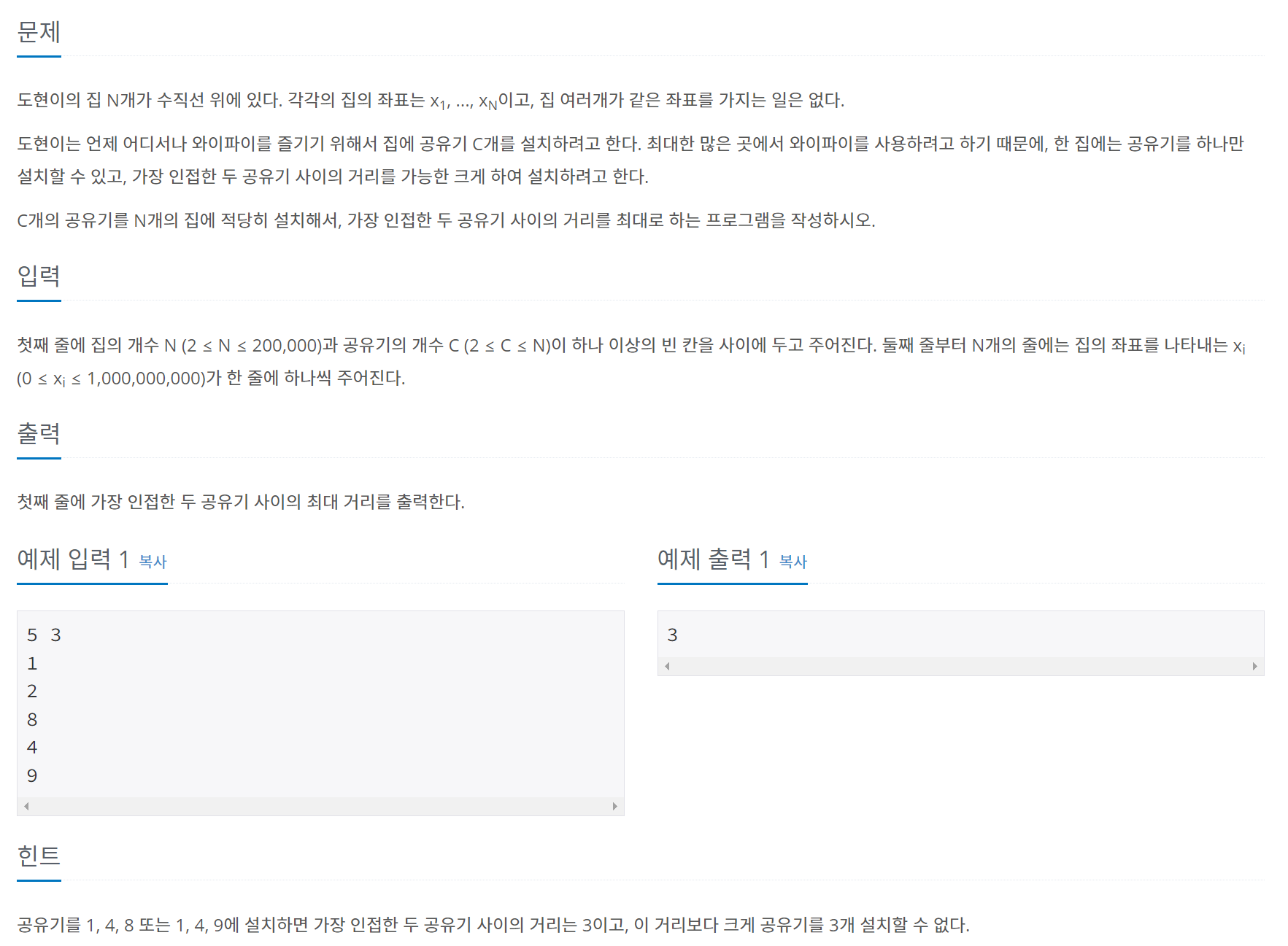
= 문제 접근 방법 ( 틀림 ) =
내가 접근한 방법은 공유기를 하나 하나 다 설치해보고 그거에 최댓값을 찾는 식으로 했었다.
애초에 끝까지 구현도 못한 방식이라 어떻게 말해야 될지 모르겠다..
이분 탐색 파트에서 1번 2번 문제는 이해했고 어떻게 접근하면 되는 건지 깨달았는데
이런식으로 조금만 문제가 다르게 나오고, 응용이 필요하면 항상 틀린다.
더 깊게 생각하고 여러 문제를 풀면서 사고력을 키워야겠다.
= 해결 =
우리가 그동안 해왔던 방식이랑 매우 비슷하다.
인덱스에서 절반을 나누고, 최댓값을 찾는 식으로 구현했었다.
이 문제도 똑같다. 단지, 응용하고 사고력이 필요했던 문제다.
주어진 식으로 최댓값을 찾냐
아니면 주어진 식을 이용해서 결과를 최대로 만드냐 ? 이런 느낌이라고 보면 된다.
숫자 찾기같은 경우에는 Uppeer Bound형식으로, 반을 나누어서 2라는 숫자를 찾는다고 생각하면
2를 초과하는 index를 구해서 몇 개인지 개수를 확인하면 되는데
공유기 설치는 내가 설치를 할 수 있을 때 까지 반복을 하는 것이다.
문제에 주어진 N => 5개의 집, C => 공유기 3개
5개 집에 공유기 3개를 설치하고 가장 인접한 두 공유기 사이의 거리를 최대로 만들어야 된다!
1. 1번 집에 무조건 설치
2. (최소 거리(1) + 최대 거리(arr[n - 1] - arr[0] + 1)) / 2 를 통해서 중간값을 구한다.
3. 이 중간값을 이용해 마지막 설치한 좌표에서 이 중간값만큼 설치하는 것이다.
4. 설치가 되면 count++, 마지막 설치한 좌표를 갱신하는 식으로 구현하면 된다.
arr[n - 1] - arr[0] + 1을 하는 이유는?
2 2
1
2
를 입력했다고 가정하자.
Upper Bound는 찾고자 하는 값을 초과하는 첫 번째 인덱스를 의미하기 때문에
Upper Bound가 최대로 가질 수 있는 값은 +1이 되어야 한다.
예제로 설명하면
int mid = (최소 거리(1) + 최대 거리(9)) / 2 = 5
1번집에는 무조건 설치,
1 ~ 2번 사이는 5보다 작기 때문에 설치 x
1 ~ 4번 사이는 5보다 작기 때문에 설치 x
1 ~ 8번 사이는 5보다 크거나 같기 때문에 설치 o
8 ~ 9번 사이는 5보다 작기 때문에 설치 x
(집 사이의 최소 거리와 집 사이의 최대 거리)
1 2 4 8 9 좌표가 있으면 최소는 1, 최대는 9를 기준으로 시작한다.
=> 2개 설치. 우리는 3개를 설치해야 되기 때문에 거리를 줄여야 한다.
end = mid;
int mid = (1 + 5) / 2 = 3 ... 이런식으로 진행한다.
그동안 이분 탐색을 다 풀었으면 충분히 이해할 수 있는 문제다.
너무 틀에 박힌 사고 방식을 갖고 있어서 이 문제로 조금 개선할 수 있도록 노력하자.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 | import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import java.util.Arrays; import java.util.StringTokenizer; public class Main { public static void main(String[] args) throws IOException { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); StringTokenizer st = new StringTokenizer(br.readLine()); int n = Integer.parseInt(st.nextToken()); // 집 n개 int c = Integer.parseInt(st.nextToken()); // 공유개 c개 int[] arr = new int[n]; int max = 0; for (int i = 0; i < n; i++) { st = new StringTokenizer(br.readLine()); arr[i] = Integer.parseInt(st.nextToken()); max = Math.max(max, arr[i]); } Arrays.sort(arr); int start = 1; int end = arr[n - 1] - arr[0] + 1; while (start < end) { int count = 0; int mid = (start + end) / 2; count++; int last = arr[0]; for (int i = 1; i < n; i++) { int location = arr[i]; if (Math.abs(last - location) >= mid) { count++; last = location; } } if (count > c) { start = mid + 1; } else if (count == c) { start = mid + 1; } else if (count < c) { end = mid; } } System.out.println(start - 1); } } | cs |
'백준 오답노트 > 이분 탐색' 카테고리의 다른 글
| 백준 - 이분 탐색 1300번 K번째 수 / 풀이, 오답 (0) | 2023.01.19 |
|---|---|
| 백준 - 이분 탐색 2805번 나무 자르기 / 풀이, 오답 (0) | 2023.01.09 |
| 백준 - 이분 탐색 1654번 랜선 자르기 / 풀이,오답 (0) | 2023.01.09 |
| 백준 - 이분 탐색 10816 숫자 카드2 문제 / 복습 (0) | 2023.01.05 |
