= 접근 과정 ( 틀림 ) =
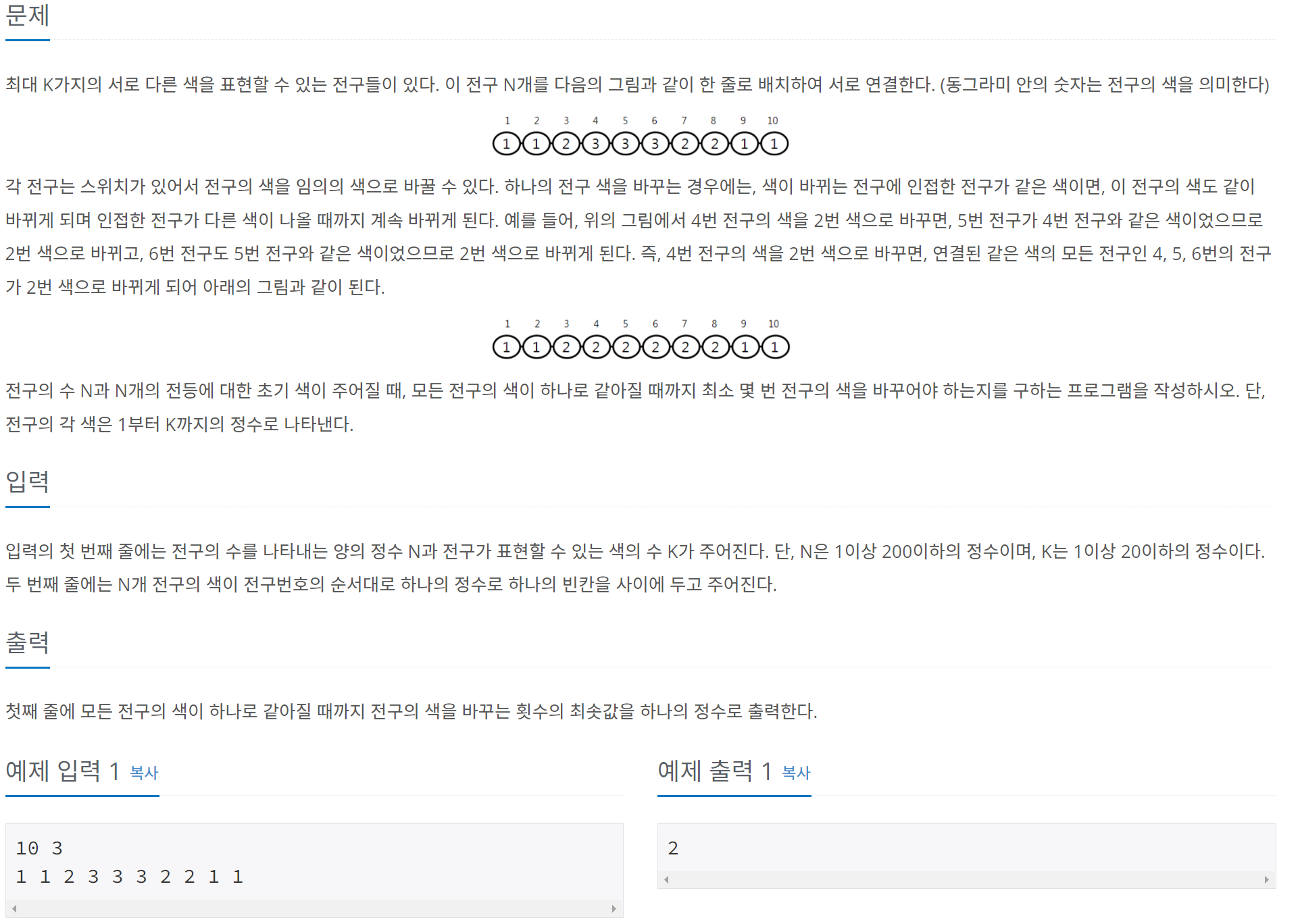
이렇게 N개의 전구와, K가지의 색 => 최대 200개의 전구, 최대 20개의 색이므로
완전 탐색을 이용하면 시간 초과로 분명히 오답! => O(N!), 이유는 N개의 색이 모두 다 다를 수 있기 때문
이러한 문제는 DP를 이용해서 시간을 줄이는게 핵심이다.
처음 나는 재귀 함수를 이용해서, 이미 거친 전구들은 return하는 형식으로 문제를 접근했다.
1. int[] arr = new int[n] 배열에 1, 1, 2, 3, 3, 3, 2, 2, 1, 1의 값을 넣고
0번 index의 값을 2로 바꿨을 때, 인접한 값(1번 index)이 0번째 값(1)이랑 같을 때 같이 2로 변경해주고 아니면 return을 하는 형식으로 count를 했다.
2. 모든 값이 k로 다 통일 되었을 때, 몇 번째 index를 변경했을 때 count가 제일 작은지 구하려고 했다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
public static void dfs(int n, int check, int k, int change) {
if (map.containsKey(check)) {
if (map.get(check) == change) {
return;
}
}
map.put(check, change);
System.out.println("check : " + check);
// 탈출 조건
if (check < 0 || check == n) {
return;
}
if (arr[check] == k) {
count++;
arr[check] = change;
} else {
return;
}
dfs(n, check - 1, k, change);
dfs(n, check + 1, k, change);
}
|
cs |
이러한 함수를... 이용해서 해결하려고 했었는데 문제가 되는 부분이 많았다. ( 내가 해결하지 못했던 문제점들)
1. 0번 index를 바꾼다고 가정을 했었는데, 값이 변할 때 마다 count를 해주는 방식 말고 이 함수가 한 번 돌았을 때를 기준으로 count했어야 하는데
이러한 방법을 생각해내지 못했다.
지금 와서 생각하는 건데 결국 0~9번 index의 값을 다 바꿔보는 식으로 함수를 짰는데 과연 이렇게 하면 시간 초과가 뜨지 않을까?
처음 내가 생각한 풀이는 k가 10개가 있고, 0번 인덱스 값이 1이라고 가정하면 0번 인덱스를 2, 3, 4, 5, 6, 7, 8, 9, 10으로 다 바꿔보는 형식의 코드를 생각했다.
너무 복잡해서 이 방법은 실패...
2. 만약 1번 문제를 해결했다고 해도, 0번 index를 2로 바꿨으니까 8or 9번 index도 결국 2로 바꿔줘야 된다.
이러한 방법을 생각하지 못해서 이 문제를 실패했다. 아직 많이 부족하다.
= 해결 방법 =
출처 : https://www.youtube.com/watch?v=kxw7FXsjxac&t=0s
그래서 유튜브를 참고해서 더 좋은 방법으로 공부를 완료
이 문제에 대해 확실하게 이해하고, 그냥 최적의 경우의 수를 구하는 방법만 생각해서 최솟값을 추출하면 된다.
나처럼 모든 경우의 수를 다 구하고 (내 풀이는 결국 완전탐색인 거 같은데?) 최솟값을 구하는 방식은 틀린 방식이였다.
정말 간단한게! 모든 최소의 경우의 수를 비교해서 최솟값을 구하면 된다!
1, 1, 2, 3, 3, 3, 2, 2, 1, 1 이라는 1차원 배열이다.
인접한 값은 어차피 변하니까 굳이 10개의 값을 다 보관하고 있을 필요가 없다.
1, 2, 3, 2, 1 이렇게 5개의 값만 보관해도 경우의 수는 똑같기 때문에 최대한 쪼개자.
idx 0 1 2 3 4 5
arr 0 1 2 3 2 1 이렇게 만들 수 있다.
dp[][]라는 2차원 배열을 생성해서, 값을 최댓값으로 초기화.
5개짜리의 전구를 size 1, 2, 3, 4, 5까지 나누어서
각각 최솟값을 구하면 된다.
1번 전구부터 시작해서 2번 전구까지 구간
1, 1의 의미는 1번 전구부터 1번 전구까지 하나의 색깔로 통일하고 앞에 있는 색으로 통합한다.
따라서 [1, 1]은 통일할 필요가 없기 때문에 0이라고 생각하면 된다.
[1, 1] [2, 2] [3, 3] [4, 4] [5, 5] => size == 1의 경우의 수를 구해보자.
0 0 0 0 0
[1, 2] [2, 3] [3, 4] [4, 5] => size == 2의 경우의 수
1, 2구간의 최솟값은 어떻게 구할 수 있을까?
[1, 1] + [2, 2] 구간을 더하면 우리가 이미 구했던 0 + 0이지만
여기서 끝이 아니다. 앞에있는 1, 2를 같은 색으로 통일는 경우의 수까지 생각해야 된다. ( 1번 전구는 색 1, 2번 전구는 색 2 서로 다른 색을 갖고있다)
따라서 [1, 1] + [2, 2] + a[1] vs a[2] => 0 + 0 + 1 이런식으로 모든 구간의 최솟값을 구하면 된다.
결국 [1,5]가 정답이 된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
|
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class ReMain {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken()); // 전구 n개
int k = Integer.parseInt(st.nextToken()); // 표현할 수 있는 색 k
int[] a = new int[n + 1];
int[][] dp = new int[n + 1][n + 1];
st = new StringTokenizer(br.readLine());
for (int i = 1; i <= n; i++) {
a[i] = Integer.parseInt(st.nextToken());
if (a[i] == a[i - 1]) { // 중복된 숫자를 빼는 과정
i--;
n--;
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) { // [1, 1] [2, 2] [3, 3]....은 어차피 경우의 수가 0이다.
dp[i][j] = Integer.MAX_VALUE;
}
dp[i][i] = 0;
}
// 식을 이용해서 dp의 값을 채워넣으면 된다.
for (int size = 2; size <= n; size++) { // 2부터 시작하는 이유는 [1, 2] [2, 3].... 을 구해야 되기 때문
for (int start = 1; start <= n - size + 1; start++) { // [1, 2] [2, 3] [3, 4] [4, 5] -> [1, 3] [2, 4] [3, 5].... 값을 채워넣기
int end = size + start - 1; // [1, 2]의 값을 구할 때, [2, 3]의 값을 구할 때 end 값 (2, 3)
for (int mid = start; mid < end; mid++) { // [1, 2]를 구할 때, [1, 1] + [2, 2]를 한다. 따라서 미드는 start, end 사이
int newValue = dp[start][mid] + dp[mid + 1][end];
if (a[start] != a[mid + 1]) {
newValue++;
}
if (dp[start][end] > newValue) {
dp[start][end] = newValue;
}
}
}
}
System.out.println("dp[1][5] = " + dp[1][n]);
}
}
|
cs |

= 접근 과정 ( 틀림 ) =
이렇게 N개의 전구와, K가지의 색 => 최대 200개의 전구, 최대 20개의 색이므로
완전 탐색을 이용하면 시간 초과로 분명히 오답! => O(N!), 이유는 N개의 색이 모두 다 다를 수 있기 때문
이러한 문제는 DP를 이용해서 시간을 줄이는게 핵심이다.
처음 나는 재귀 함수를 이용해서, 이미 거친 전구들은 return하는 형식으로 문제를 접근했다.
1. int[] arr = new int[n] 배열에 1, 1, 2, 3, 3, 3, 2, 2, 1, 1의 값을 넣고
0번 index의 값을 2로 바꿨을 때, 인접한 값(1번 index)이 0번째 값(1)이랑 같을 때 같이 2로 변경해주고 아니면 return을 하는 형식으로 count를 했다.
2. 모든 값이 k로 다 통일 되었을 때, 몇 번째 index를 변경했을 때 count가 제일 작은지 구하려고 했다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
public static void dfs(int n, int check, int k, int change) {
if (map.containsKey(check)) {
if (map.get(check) == change) {
return;
}
}
map.put(check, change);
System.out.println("check : " + check);
// 탈출 조건
if (check < 0 || check == n) {
return;
}
if (arr[check] == k) {
count++;
arr[check] = change;
} else {
return;
}
dfs(n, check - 1, k, change);
dfs(n, check + 1, k, change);
}
|
cs |
이러한 함수를... 이용해서 해결하려고 했었는데 문제가 되는 부분이 많았다. ( 내가 해결하지 못했던 문제점들)
1. 0번 index를 바꾼다고 가정을 했었는데, 값이 변할 때 마다 count를 해주는 방식 말고 이 함수가 한 번 돌았을 때를 기준으로 count했어야 하는데
이러한 방법을 생각해내지 못했다.
지금 와서 생각하는 건데 결국 0~9번 index의 값을 다 바꿔보는 식으로 함수를 짰는데 과연 이렇게 하면 시간 초과가 뜨지 않을까?
처음 내가 생각한 풀이는 k가 10개가 있고, 0번 인덱스 값이 1이라고 가정하면 0번 인덱스를 2, 3, 4, 5, 6, 7, 8, 9, 10으로 다 바꿔보는 형식의 코드를 생각했다.
너무 복잡해서 이 방법은 실패...
2. 만약 1번 문제를 해결했다고 해도, 0번 index를 2로 바꿨으니까 8or 9번 index도 결국 2로 바꿔줘야 된다.
이러한 방법을 생각하지 못해서 이 문제를 실패했다. 아직 많이 부족하다.
= 해결 방법 =
출처 : https://www.youtube.com/watch?v=kxw7FXsjxac&t=0s
그래서 유튜브를 참고해서 더 좋은 방법으로 공부를 완료
이 문제에 대해 확실하게 이해하고, 그냥 최적의 경우의 수를 구하는 방법만 생각해서 최솟값을 추출하면 된다.
나처럼 모든 경우의 수를 다 구하고 (내 풀이는 결국 완전탐색인 거 같은데?) 최솟값을 구하는 방식은 틀린 방식이였다.
정말 간단한게! 모든 최소의 경우의 수를 비교해서 최솟값을 구하면 된다!
1, 1, 2, 3, 3, 3, 2, 2, 1, 1 이라는 1차원 배열이다.
인접한 값은 어차피 변하니까 굳이 10개의 값을 다 보관하고 있을 필요가 없다.
1, 2, 3, 2, 1 이렇게 5개의 값만 보관해도 경우의 수는 똑같기 때문에 최대한 쪼개자.
idx 0 1 2 3 4 5
arr 0 1 2 3 2 1 이렇게 만들 수 있다.
dp[][]라는 2차원 배열을 생성해서, 값을 최댓값으로 초기화.
5개짜리의 전구를 size 1, 2, 3, 4, 5까지 나누어서
각각 최솟값을 구하면 된다.
1번 전구부터 시작해서 2번 전구까지 구간
1, 1의 의미는 1번 전구부터 1번 전구까지 하나의 색깔로 통일하고 앞에 있는 색으로 통합한다.
따라서 [1, 1]은 통일할 필요가 없기 때문에 0이라고 생각하면 된다.
[1, 1] [2, 2] [3, 3] [4, 4] [5, 5] => size == 1의 경우의 수를 구해보자.
0 0 0 0 0
[1, 2] [2, 3] [3, 4] [4, 5] => size == 2의 경우의 수
1, 2구간의 최솟값은 어떻게 구할 수 있을까?
[1, 1] + [2, 2] 구간을 더하면 우리가 이미 구했던 0 + 0이지만
여기서 끝이 아니다. 앞에있는 1, 2를 같은 색으로 통일는 경우의 수까지 생각해야 된다. ( 1번 전구는 색 1, 2번 전구는 색 2 서로 다른 색을 갖고있다)
따라서 [1, 1] + [2, 2] + a[1] vs a[2] => 0 + 0 + 1 이런식으로 모든 구간의 최솟값을 구하면 된다.
결국 [1,5]가 정답이 된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
|
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class ReMain {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken()); // 전구 n개
int k = Integer.parseInt(st.nextToken()); // 표현할 수 있는 색 k
int[] a = new int[n + 1];
int[][] dp = new int[n + 1][n + 1];
st = new StringTokenizer(br.readLine());
for (int i = 1; i <= n; i++) {
a[i] = Integer.parseInt(st.nextToken());
if (a[i] == a[i - 1]) { // 중복된 숫자를 빼는 과정
i--;
n--;
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) { // [1, 1] [2, 2] [3, 3]....은 어차피 경우의 수가 0이다.
dp[i][j] = Integer.MAX_VALUE;
}
dp[i][i] = 0;
}
// 식을 이용해서 dp의 값을 채워넣으면 된다.
for (int size = 2; size <= n; size++) { // 2부터 시작하는 이유는 [1, 2] [2, 3].... 을 구해야 되기 때문
for (int start = 1; start <= n - size + 1; start++) { // [1, 2] [2, 3] [3, 4] [4, 5] -> [1, 3] [2, 4] [3, 5].... 값을 채워넣기
int end = size + start - 1; // [1, 2]의 값을 구할 때, [2, 3]의 값을 구할 때 end 값 (2, 3)
for (int mid = start; mid < end; mid++) { // [1, 2]를 구할 때, [1, 1] + [2, 2]를 한다. 따라서 미드는 start, end 사이
int newValue = dp[start][mid] + dp[mid + 1][end];
if (a[start] != a[mid + 1]) {
newValue++;
}
if (dp[start][end] > newValue) {
dp[start][end] = newValue;
}
}
}
}
System.out.println("dp[1][5] = " + dp[1][n]);
}
}
|
cs |
