에라토스테네스의 체 알고리즘 - 소수 구하기 알고리즘

우리는 에라토스테네스의 체(Sieve of Eratosthenes)라는 방법을 통해 보다 쉽게 소수를 찾아낼 수 있습니다. 이름 그대로 체를 통해 무언가를 걸러내듯이 소수를 찾는 방법입니다.

 

일반적으로 소수만 구하려면 2중 for문을 이용해 시간 복잡도는 O(N^2)라고 판단할 수 있다.
에라토스테네스의 체 알고리즘을 이용하면 시간 복잡도는 O(Nlog(logN))이다.

배수를 삭제하는 연산으로 바깥 for문을 생략하는 경우가 발생하기 때문이다.

1. 찾을 범위까지 수를 나열한 다음, 소수가 아닌 1을 지웁니다.
2. 1 다음으로 큰 소수인 2를 남겨두고 2의 배수를 모두 지웁니다.
3. 2 다음으로 큰 소수인 3을 남겨두고 3의 배수를 모두 지웁니다.
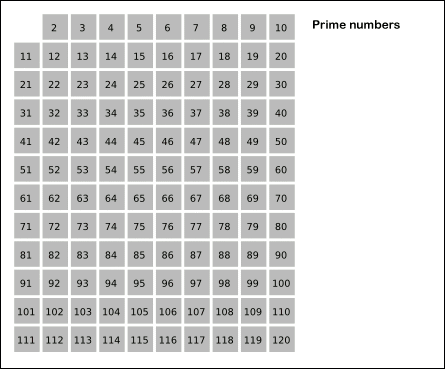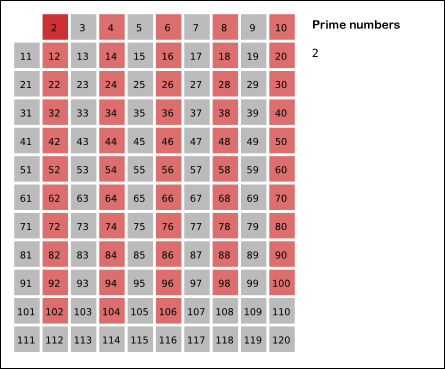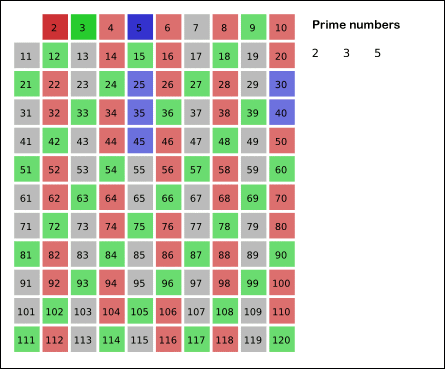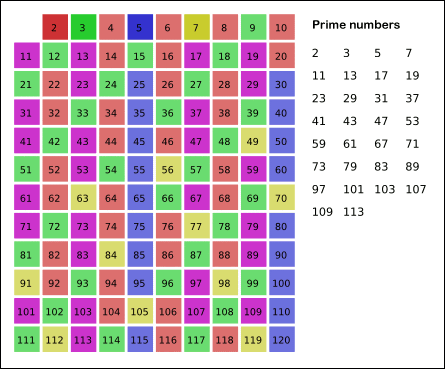
4. prime(n) 다음으로 큰 소수인 prime(n+1)을 남겨두고 prime(n+1)의 배수를 모두 지웁니다.
5. 더 이상 지울 수 없을 때, 남아있는 수들이 소수입니다.

출처: 위키백과

= 간단한 코드 =

int n = Integer.parseInt(br.readLine());
 
        int[] arr = new int[n + 1];
 
        for (int i = 2; i <= n; i++) { // 첫 for문
            arr[i] = i;
        }
 
        for (int i = 2; i <= n; i++) {
            if (arr[i] == 0) {
                continue;
            }
            for (int j = i + i; j <= n; j+=i) {
                arr[j] = 0;
            }
        }

n = 20 이라고 가정해보자

 

1. 배열은 당연히 n + 1 크기로 생성

(int 배열은 값을 정해주지 않으면 기본으로 0이 들어감)

 

2. 0, 1은 소수가 아니기 때문에 기본 값인 0으로 해놓고 2부터 첫 for문을 이용해 i값을 넣어준다.

=> arr[2] = 2, arr[3] = 3, arr[4] = 4, arr[5] = 5, arr[6] = 6 . . ....... 이런 식으로

 

3. 처음으로 선택 된 수 ( 2, 3 ...은 소수이기 때문에 소수의 배수부터 제거, 즉 0으로 만든다 )

i = 2일 때, j = 4; j <= 20; j += i 이기 때문에

 

4, 6, 8, 10, 12, 14, 16, 18, 20 이런 순서로 지워질 것이고

 

i = 3일 때, j = 6; j <= 20; j += i 이기 때문에

 

6, 9, 12, 15, 18 이런 순서로 지워진다.

 

따라서 남는 수, 즉 0이 아닌 수는 소수가 된다는 것임.

 

if ( arr[i] == 0 ) continue를 사용한 이유는

어차피 배수로 지워진 숫자들의 배수를 해도 똑같기 때문에 시간을 줄일 수 있는 것이다.

 

예를들면 i = 4일 때를 생각해보자

i = 4일 때, j = 8; j <= 20; j += i 

 

8, 12, 16, 20 이 과정은 어차피 i = 2일 때 이미 진행했기 때문에 이 과정을 스킵함으로써

시간 복잡도가 O(Nlog(logN))이 나오는 것임!

 

설명이 조금 난잡할 수 있지만 필요한 핵심 설명은 완료!