투 포인터 개념
각 원소마다 모든 값을 순회해야할 때,
*연속하다는 특성을 이용해서 처리,
단순 반복문을 이용해서 문제를 해결하려고 하면, 시간 복잡도가 O(N^2), O(N^3)인 경우가 있기 때문에 투 포인터 알고리즘을 이용해서 문제를 해결해야 된다.
포인터 2개가 1차원 배열을 증가하는 방향으로만 순회하므로 O(N) + O(N) = O(N)
이 알고리즘을 처음 접했을 때 어려웠는데 이제는 기본적인 문제는 풀 수 있게 되었다. 그만큼 계속 반복함!
https://www.acmicpc.net/problem/2003 이 문제를 기반으로 설명을 하겠따.
n개로 나열 된 수, +해서 m이되는 경우의 수를 구하자
- 자연수로 이루어진 1차원 배열이 주어진다.
- 연속되는 부분 배열 중 원소의 합이 M이 되는 경우의 수를 구하는 문제
= 접근 방법 =
1. 초기 포인터를 2개 설정 => 0으로 초기화.
2. start ~ end에 포함되는 구간은 현재 부분 배열이다.
3. start는 항상 end보다 작거나 같아야 함.
4. 포인터는 항상 증가한다.
= 포인터가 움직일 때 =
1. 현재 부분 배열의 합이 M보다 작을 때, => end++
2. 현재 부분 배열의 합이 M보다 클 때, => start++
3. 현재 부분 배열의 합이 M과 같을 때, => end++
= 문제 + 그림을 통한 자세한 설명 =





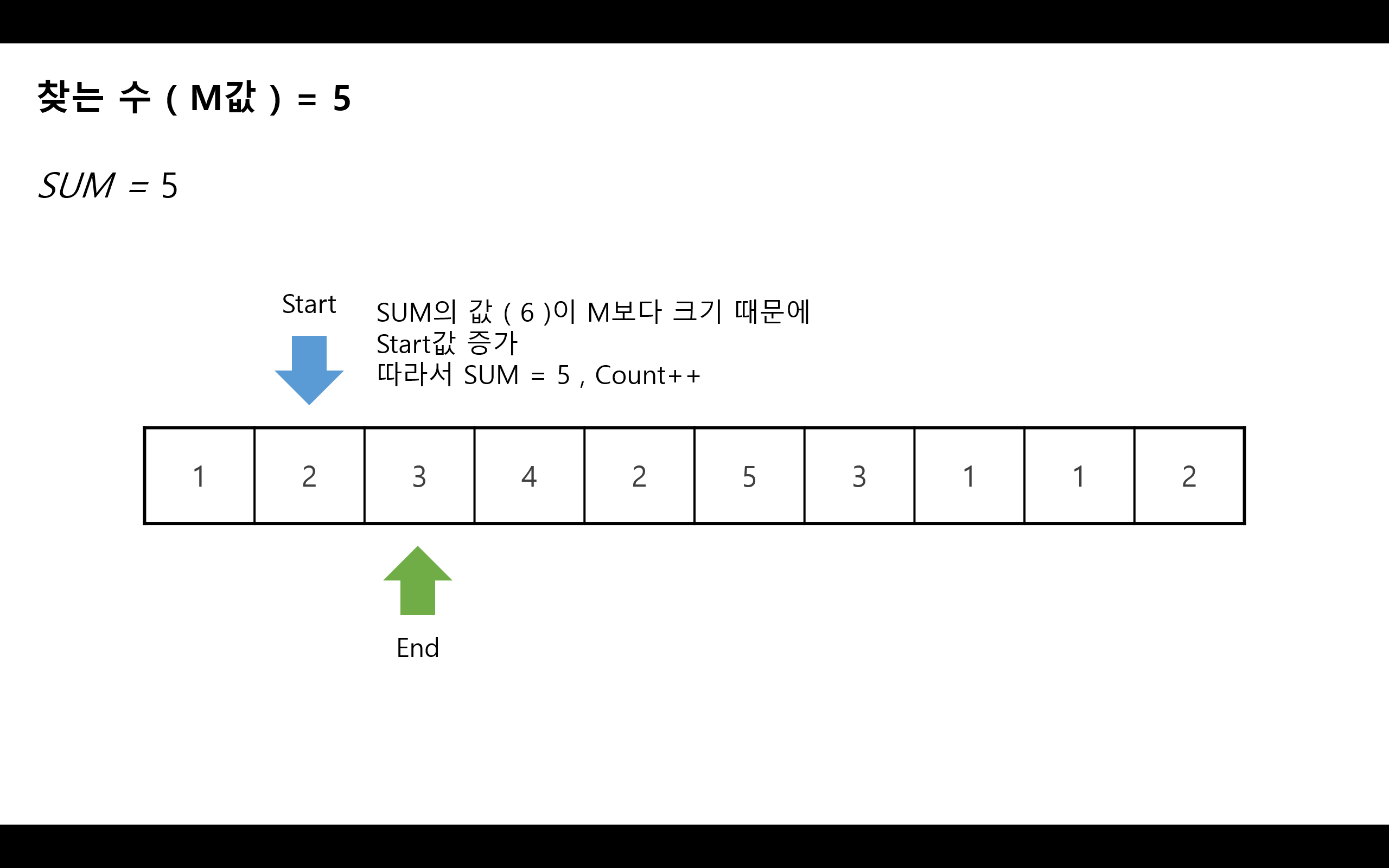
이런식으로 하나하나씩 찾는 과정이라고 생각하면 된다.

N = 10, M = 5, => 10개 나열 된 수를 이용해서 합했을 때 5가 되는 경우의 수를 구하면 된다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
// 1. input
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
int[] arr = new int[n];
st = new StringTokenizer(br.readLine());
for (int i = 0; i < n; i++) {
arr[i] = Integer.parseInt(st.nextToken());
} // 여기까지, 입력
int start = 0; // 왼쪽 index
int end = 0; // 오른쪽 index
int count = 0; // K = 5일 때, count를 1개씩 증가
int sum = 0;
while (start < n && end < n) {
sum = 0;
for (int i = start; i <= end; i++) {
sum += arr[i];
}
if (sum < k) {
end++;
} else if (sum > k) {
start++;
} else if (sum == k) {
count++;
end++;
}
}
System.out.println(count);
}
}
간단하게 구현 끝!
