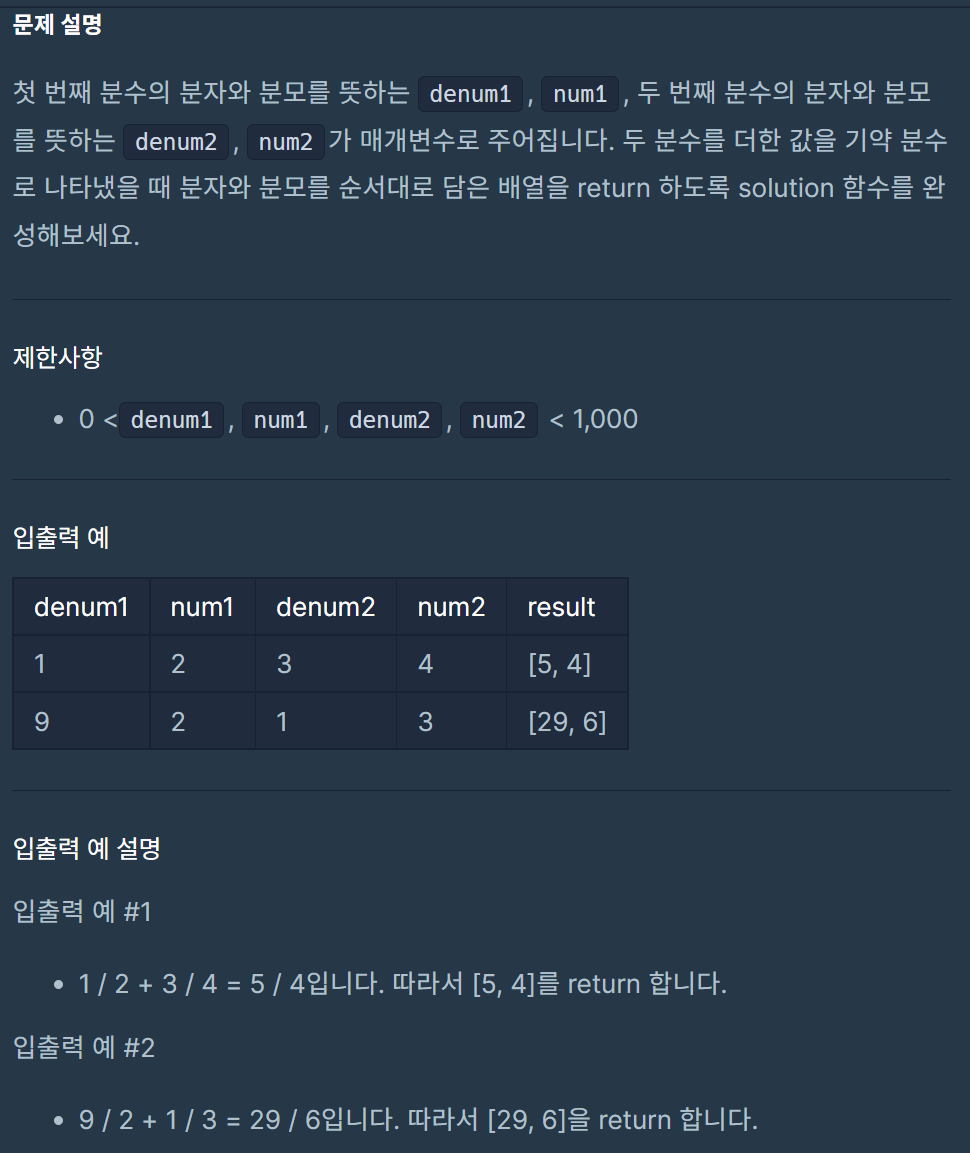
= 내가 푼 방법 ( 틀림 ) =
이렇게 복잡하게 풀어도 틀렸다.
내가 접근한 방법은
1. 두 분수를 비교해서 분모가 더 큰 곳을 찾는다.
1-1. 분모가 같을 경우 그냥 분자끼리 더하고 출력
2. 분모가 작은 쪽을 더 큰 분모에 맞춘다 ( 통분 )
2-2. 만약 하나의 분모로 통분이 안 된다면 분모 각각 곱하는 식으로 통분
3. 그렇게해서 값을 출력
=> 오답,
약분을 안 해준 것도 오답의 원인 중 하나
정확하게 어떤 부분에서 틀렸는지 모르겠다.
이러한 복잡한 방식으로 해결하면 안 될 것 같다.
모든 경우의 수를 다 생각해서 값을 구하는 거는 정답을 맞출 순 있어도 너무 비효율적이다.
= 다른 풀이 =
1 / 2 값과 3 / 4 값을 그냥 더하면 어떻게 구할 수 있을까?
denum1 = 1, num1 = 2
denum2 = 3, num2 = 4
우리가 흔하게 사용하던 수학으로 접근하면 denum1 * num2 / num1 * num2 + denum2 * num1 / num1 * num2
이렇게 간단하게 사용할 수 있다. 난 이 생각을 못했다...
이렇게 하고 약분만 해주면 답이다.
근데 약분을 어떻게 할 수 있을까?
num1 과 num2의 최대공약수를 구해서 나눠주기만 하면 끝!
재귀 방식을 이용한다 ( 유클리드 호제법 ) 나중에 사용 할 일이 있으니까 이 알고리즘은 꼭 숙지한다!
https://st-lab.tistory.com/154 정확한 해설은 이 블로그를 참고하면 된다.
CD(581, 322)일 때 r(나머지) = 259이다. 즉, GCD(581, 322) = GCD(322, 259)이다.그럼 다시 GCD(322, 259)를 보면 r=63이다. 그러면 GCD(322, 259) = GCD(259, 63)이다.또 다시 GCD(259, 63)을 보면 r=7이다. 즉, GCD(259, 63) = GCD(63, 7)이다.
다시 GCD(63, 7)을 보면 r=0 이다. 그러면 GCD(63, 7) = GCD(7, 0)이다.
결과적으로 나머지가 없다는 것은 공통된 약수로 나누어 떨어진다는 의미이므로 7이 최대공약수가 된다. 쉽게 쓰면 이렇다.
GCD(581, 322) = GCD(322, 259) = GCD(259, 63) = GCD(63, 7) = GCD(7, 0) = 7
두 수의 최대 공약수를 구하는 코드를 보자
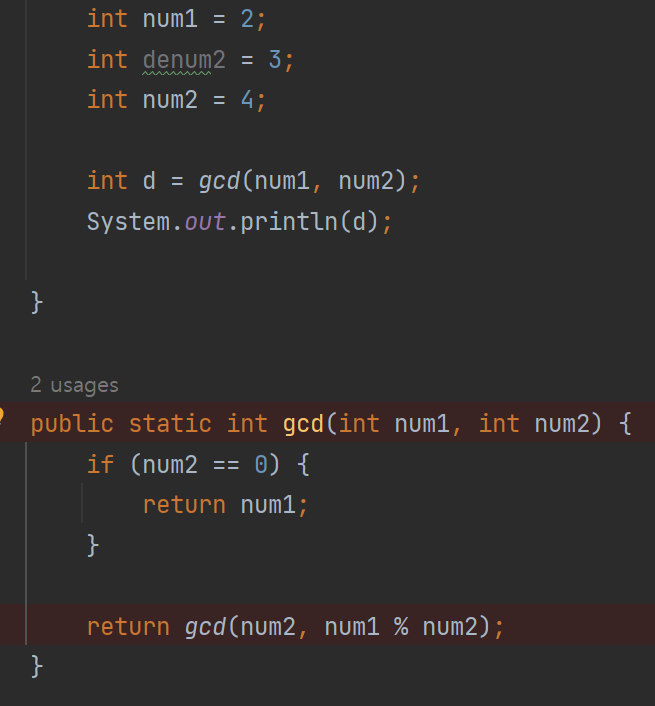
순서대로 2, 4를 입력
num2 == 0 이 아니기 때문에 return gcd(num2, num1 % num2) 실행
num2는 4였고, 두번째 값이 num1로 넘어오고, 다시 num2는 num1 % num2의 값이기 때문에
계속 나머지를 구하다보면 0일 때, 그 때 return을 해주면 최대 공약수를 구할 수 있다.
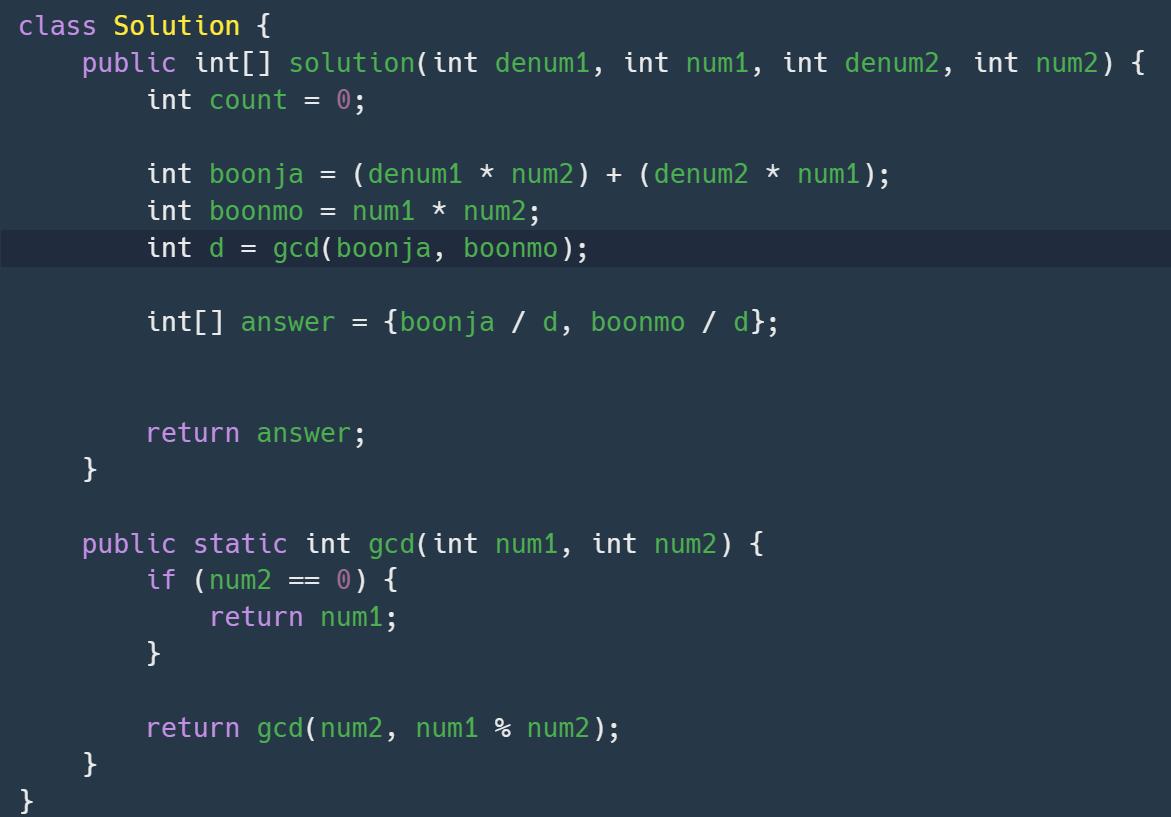
이렇게 해서 최대공약수를 구한 다음
denum1 * num2 / num1 * num2 + denum2 * num1 / num1 * num2 이 값에 / 최대공약수만 해주면 끝!
레벨0인 문제도 완벽히 해결하지 못하는데 더 열심히 노력하자.
'프로그래머스 > Level: 0' 카테고리의 다른 글
| 프로그래머스 - Level: 0 - 겹치는 선분의 길이 (0) | 2022.12.13 |
|---|
