백준 오답노트/투 포인터
백준 - 투 포인터 1806번 부분합 / 문제풀이, 오답노트
초보병일이
2022. 12. 28. 09:42
728x90
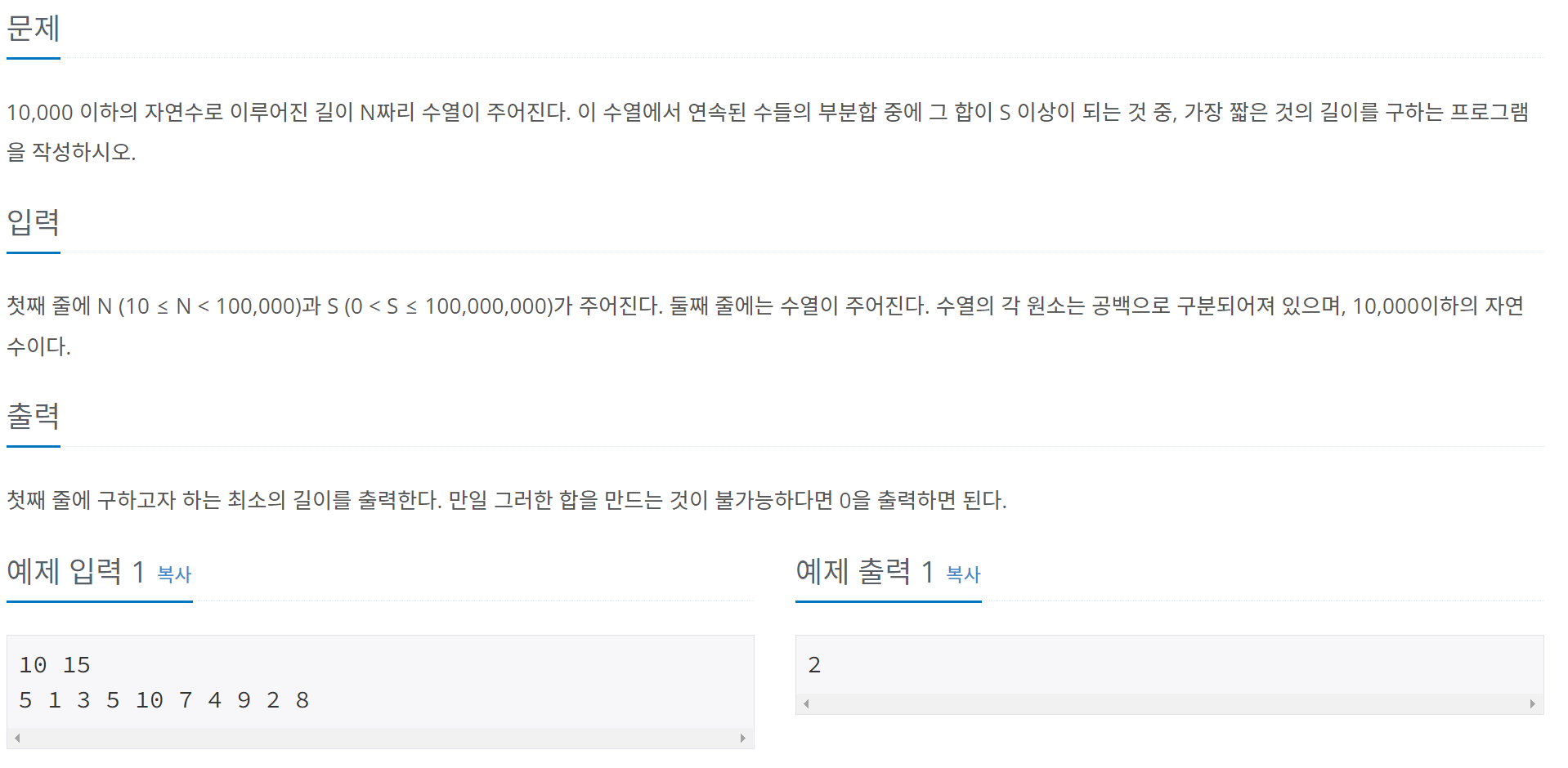
투 포인터 알고리즘을 이용해서 해결하는 문제.
= 내가 틀린 이유 =
시간 초과로 틀렸다.
while문 안에 for문을 이용해서 코드를 짰는데, 이렇게 하면 시간 복잡도는 O(NlogN)
while문 하나만 이용해서 O(N)을 만들어야 해결할 수 있는 문제다.
= 접근 방법 =
1. 부분합을 구하는 문제이기 때문에 정렬할 필요 x
2. 투 포인터 알고리즘을 이용해서 부분합 구한 후, 최솟값을 계속 갱신
3. while문 종료 조건을 if (sum >= s) 이후, else if에 end == n을 사용하는 이유는?
예제 입력 1에 9, 2, 8 부분을 보면
9, 2, 8일 때, 19이고 if (sum >= s) 를 타고
2, 8이 된다. 그리고 end == n 이라는 조건을 만나서 while문 종료
따라서 end를 최대한 이용할 수 있을 때 까지 이용하기 위해서 이러한 조건을 사용하는 것이다.
만약 while 문 안에 end != n이라고 했을 때는 sum >= s 라는 조건을 수행하지 못하고 종료되기 때문에
마지막 값을 구할 수 없는 것이다.
시간 초과 + 이러한 문제때문에 오답이 나왔는데 이번 기회에 하나 하나 코드로 다 찍어보고
분석해보면서 투 포인터를 더 잘 알게 되었다!
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main2 {
public static void main(String[] args) throws IOException {
// 1. input
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken()); // 길이 n
int s = Integer.parseInt(st.nextToken()); // 합
int[] arr = new int[n];
st = new StringTokenizer(br.readLine());
for (int i = 0; i < n; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
int answer = 0;
answer = minLength(arr, s, n);
if (answer == Integer.MAX_VALUE) {
System.out.println(0);
} else {
System.out.println(answer);
}
}
// 합이 s가 되는 것 중, 가장 짧은 길이를 구하는 메서드
public static int minLength(int[] arr, int s, int n) {
int start = 0; // 시작 인덱스
int end = 0; // 끝 인덱스
int min = Integer.MAX_VALUE; // 최솟값
int sum = 0; // 부분합
while (true) {
if (sum >= s) {
min = Math.min(min, (end - start)); // 부분합이 s이상일 경우 최소 길이
sum -= arr[start++];
} else if (end == n) {
break;
} else if (sum < s) {
sum += arr[end++];
}
}
return min;
}
}
|
cs |
728x90