백준 - 기본 수학1 2869번 달팽이는 올라가고 싶다 / 구글로 해결
문제
땅 위에 달팽이가 있다. 이 달팽이는 높이가 V미터인 나무 막대를 올라갈 것이다.
달팽이는 낮에 A미터 올라갈 수 있다. 하지만, 밤에 잠을 자는 동안 B미터 미끄러진다. 또, 정상에 올라간 후에는 미끄러지지 않는다.
달팽이가 나무 막대를 모두 올라가려면, 며칠이 걸리는지 구하는 프로그램을 작성하시오.
입력
첫째 줄에 세 정수 A, B, V가 공백으로 구분되어서 주어진다. (1 ≤ B < A ≤ V ≤ 1,000,000,000)
출력
첫째 줄에 달팽이가 나무 막대를 모두 올라가는데 며칠이 걸리는지 출력한다.
예제 입력 1 복사
2 1 5
예제 출력 1 복사
4
예제 입력 2 복사
5 1 6
예제 출력 2 복사
2
예제 입력 3 복사
100 99 1000000000
예제 출력 3 복사
999999901
기본 수학1 부분이 난이도 자체가 높은 거는 아닌데 난 되게 어려웠다.
지금까지 4번까지 문제를 풀면서 1번을 제외한 나머지 3개는 접근도 제대로 하지 못했다.
사고력이 많이 부족한게 느껴진다.
= 해설 =
https://st-lab.tistory.com/75 이 블로그를 참고했다. 항상 감사합니다.
낮에 A만큼을 올라가고, 정상 ( V )이 아니면 저녁에 B만큼 내려간다.
V / ( A - B )로 풀면 100%틀린다.
A B V 순으로 2, 1, 5로 주어졌을 때, 5 / ( 2 - 1 ) = > 5 / 1을 하면 5일이 걸린다고 나오는데 정답은 4일이다.
정상에 도착했을 때, 내려오지 않기 때문에 그거까지 생각해서 계산을 해줘야한다.
V에서 B값을 빼주면 최소 일수를 구할 수 있다.
즉, up 과 down 의 차를 length 에서 나누면 잔여블록과 상관 없이 무조건 몫만 반환하게 된다.
근데, 문제에서 분명히 정점에 도달하면 미끄러지지 않는다는 조건이 붙어있다.
즉, 잔여 블록이 없으면 문제가 안되지만, 만약에 잔여블록이 있다면? 그러면 한 번 다시 미끄러진 다음에 올라가야 한다는 것이다.
이로써 up-down 의 차이 값보다 작은 나머지가 존재하면 다음날 up 때 올라가야하는 경우가 발생한다.
결과적으로 down 을 뺌으로서 up 과 down 의 차이를 나눈 몫은 최소한의 일(日) 수가 된다.
그리고 나머지에 대해서는 다음과 같은 두 가지 상황이 생긴다.
- ( length - down ) % ( up - down ) 가 정확하게 0 으로 떨어지는 경우
- ( length - down ) % ( up - down ) 가 나머지가 남는 경우
위 예시로 본다면 아래와 같다.
- ( 7 - 1 ) % ( 3 - 1 ) = 0
- ( 8 - 1 ) % ( 3 - 1 ) = 1
전체 길이에서 down 값을 빼고, up - down 을 나누면 둘 다 몫은 3 이다.
( 7 - 1 ) / ( 3 - 1 ) = 3
( 8 - 1 ) / ( 3 - 1 ) = 3
그러나 길이가 8일 경우 down 을 빼고 ( up - down ) 을 했는데 나머지가 생긴다.
이유는 up 과 down 의 차이 값으로 정확히 나누어 떨어지는 것이 아니라 아직 잔여 블럭이 남았기 때문이다.
그렇기 때문에 down 을 한 번 더 하게 되고, 자연스레 up 또한 한 번 더 하게 되는 것이다.
즉, 하루가 더 소요 되는 것이다.
그렇기 때문에 다음과 같이 조건문에 따라 출력값이 달라진다는 것이다.
= 코드 =
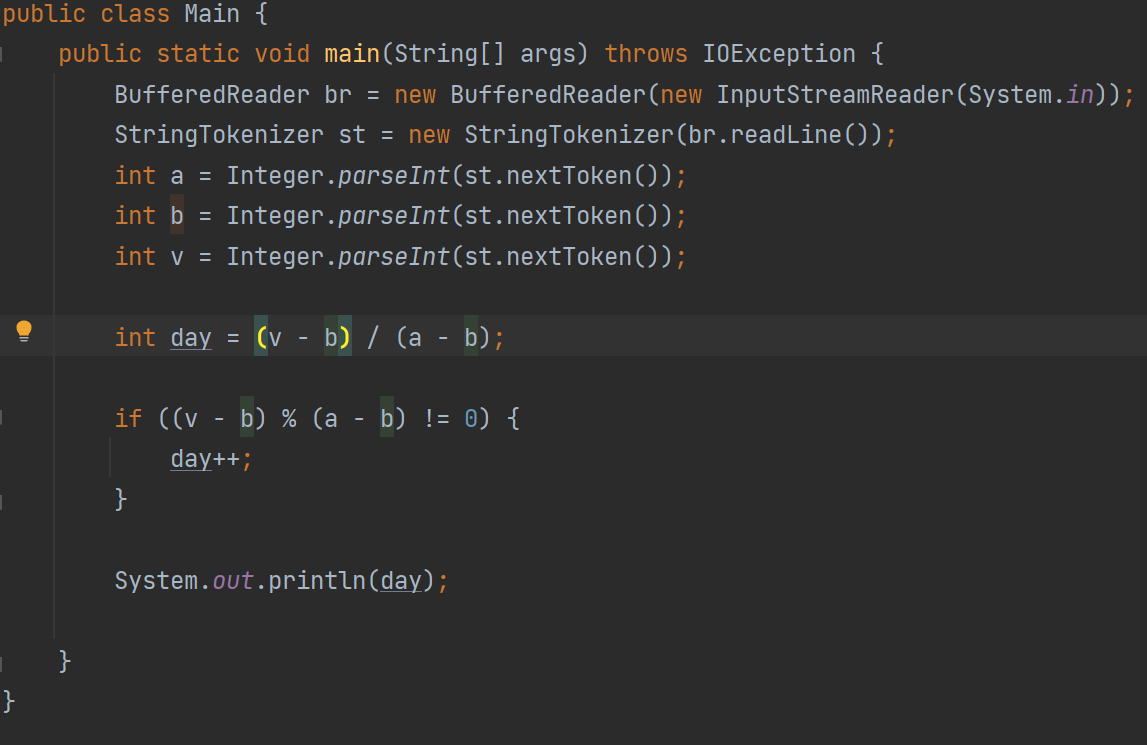
정말 어렵다..
총 길이 V에서 저녁에 내려오는 B값을 빼준다는게 아직도 잘 이해가 안 된다.
더 열심히하자.
낮에 최대 치는 nA - ( n -1 ) B > V 라고 생각하면 쉽다.
down 즉, 내려가는 것은 항상 up보다 down이 1번 적다
이러한 규칙을 발견하고 활용할 수 있는지 중요한 문제였다.